Facebook激进地使用卷积网络处理NLP问题,意外地取得了很不错的效果。而 Google 一不做二不休,发布了一种新型的网络结构,transformer模型 [1],该网络结构既不使用RNN,也不使用CNN,而且也获得不错的效果。
1. 模型结构
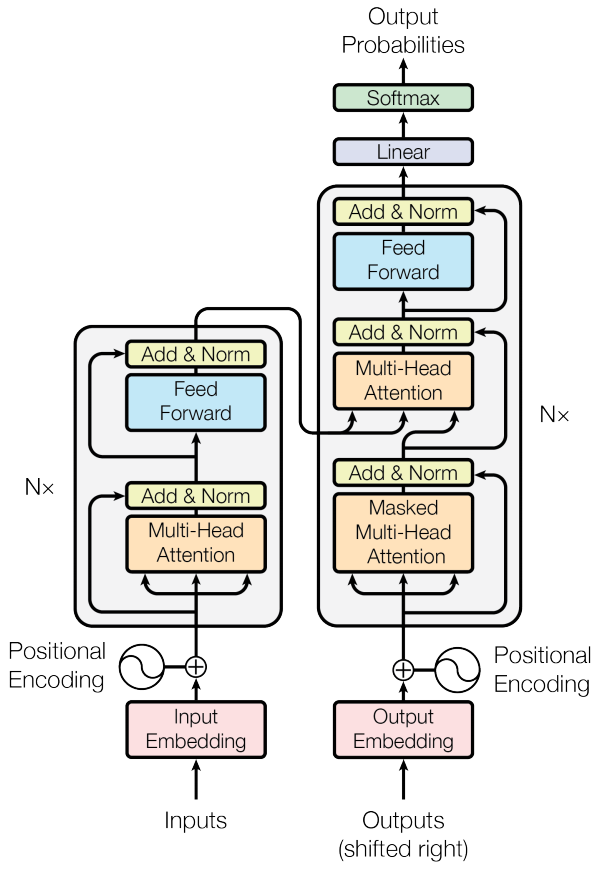
Encoder和Decoder都是从下往上的栈结构。
1.1 Encoder
Encoder有6个相同的独立层,每层有2个子层。第一个子层是多头自注意力层(multi-head self-attention),第二个子层是前馈传播层。
1.2 Decoder
Decoder同样有6个相同的独立层,每层有3个子层。第一个子层是遮罩了未来信息的多头自注意力层,第二个子层是联合encoder最后一层的输出的多头注意力层,第三个子层是前馈传播层。
下图是当只有1个独立层时候的网络结构 [1]:
1.3 注意力
注意力函数从 Query, Key, Value 映射到一个输出,这里的 Query, Key, Value 是什么可以先不管,先理解注意力模型的构造。
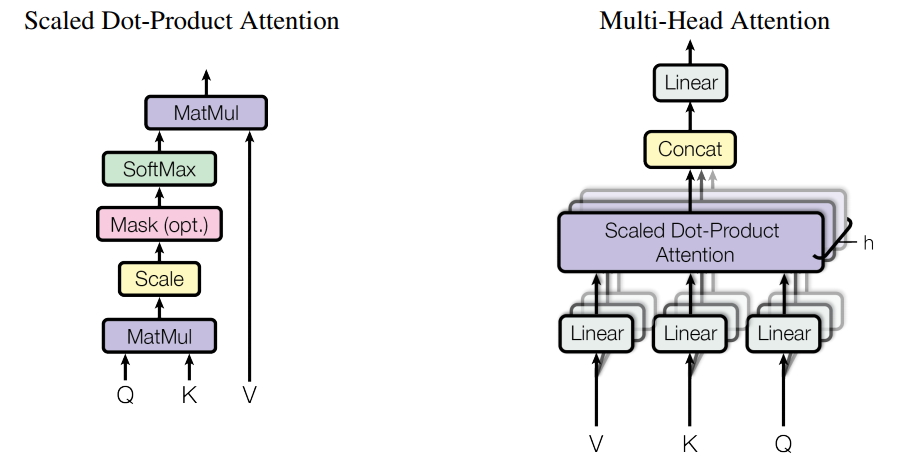
1.3.1 缩放的点积注意力 (Scaled Dot-Product Attention )
假设 query, key, value 描述为矩阵 \(\large Q, K, V\), query 和 key 的特征维度是 \(\large d_k\),而 value 的特征维度是 \(\large d_v\),那么缩放的点积注意力函数为,
\[ Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V \]
1.3.2 多头注意力(Multi-Head Attention)
把 query, key, value 从一个大的特征维度映射出多个小特征维度,由 \(\large d_{model}\) 映射到若干个 \(\large d_k\) 或 \(\large d_v\),假设有 \(\large h\) 个head,那么就有 \(\large d_k = d_v = d_{model}/h\),每一个 head 进行一次 Scaled Dot-Product Attention,最后再把所有head连接回 \(\large d_{model}\) 维度。
注意力结构如下图:
那么 query, key, value 到底是什么呢?联系上面的模型结构图。
- 对于encoder来说,第一层输入的 query, key, value 三者皆是源句子的词向量,而后面的层的输入就是上一层的输出。
- decoder的第一个子层和encoder相同,三者皆是目标句子的词向量,但是有一个Masked的标识,说明对于decoder来说,我们需要消除该词汇位置往后的参数的影响,消除方法是设置参数为负无穷。
- decoder的第二个子层中,query 是第一个子层的输出,key 和 value 是encoder 最后一层的输出。
1.4 前馈传播网络
前馈传播网络包含两个线性层, 计算如下:
\[ FFN(x) = f_2(ReLU(f_1(x))) \]
1.5 位置编码(Positional Encoding)
一个非RNN的模型无法很好的判断一个词汇在句子中的位置,解决办法是为词向量附加一个位置参数,使得模型能够学习和判断词汇的位置。论文中提出了一个使用余弦和正弦曲线的方法, \[ PE(pos, 2i)=sin(pos/10000^{2i/d_{model}}) \\ PE(pos, 2i+1)=cos(pos/10000^{2i/d_{model}}) \] 其中 \(\large pos\) 为词在序列的位置,\(\large i\) 为词向量的维度,最后的编码矩阵 \(\large PE \in \mathbb{R}^{T \times E}\)。
假设当前序列长 \(\large t\) ,那么词向量为 \(\large emb + PE(t) \rightarrow emb \in \mathbb{R}^{t \times E}\) 。
函数对于维度的数值是区分偶数和奇数的,以偶数为例,当位置为1, 5, 10时,位置向量的曲线如图所示,
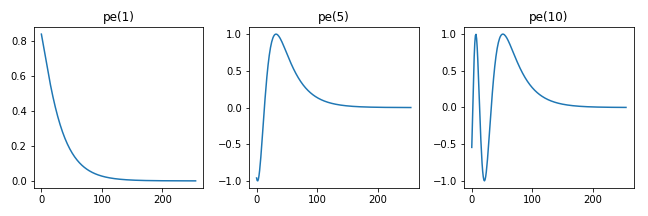
可以发现,不同位置会进行不同的线性变换,模型会学习到不同位置的固有位置向量,当词向量附加了某一位置向量后,模型就能知道该词在句子中的所在位置。
2. 详细过程
前面大概讲了一下结构和概念,但实际实现模型时还是有很多细节需要弄懂。
源句子的最大序列长度为 \(\large T\), 目标句子的最大序列长度为 \(\large T'\),批次大小为 \(\large B\),词向量大小为 \(\large E\), 源语言词汇数量为 \(\large V\),目标语言词汇数量为 \(\large V'\)。
2.1 Encoder
计算整个句子的词向量为 \(\large dropout(s \cdot emb(x) + emb\_pos(x)) \rightarrow X \in \mathbb{R}^{B \times T \times E}\),\(\large s\) 为 \(\large \sqrt{E}\)
进入第一子层,记录残差 \(\large R \leftarrow X\),标准化 \(\large X \leftarrow Norm(X)\)
把 \(\large X\) 作为query, key, value,输入自注意力层 \(\large Atten(X, X, X) \rightarrow X \in \mathbb{R}^{B \times T \times D}\),维度 \(\large D\) 即 \(\large d_{model}\)
,和词向量大小 \(\large E\) 是一样的
dropout 正则化后加上残差 \(\large X \leftarrow dropout(X) + R\)
进入第二子层,记录残差 \(\large R \leftarrow X\),标准化 \(\large X \leftarrow Norm(X)\)
输入到前馈传播网络,再加上残差 \(\large X \leftarrow FFN(X) + R\)
从步骤 (2) 到 (6) 就结束一个层了,多个层则做同样计算即可。
最终输出为 \(\large O \in \mathbb{R}^{B \times T \times E}\)
2.2 Decoder
Decoder 的第一个子层和第三个子层的步骤和encoder基本相同,这里列出第二子层的过程
记录残差 \(\large R \leftarrow X \in \mathbb{R}^{B \times T' \times E}\) [2],标准化 \(\large X \leftarrow Norm(X)\) [3]
需要输入到另外一个自注意力层中 \(\large Atten(X, O, O) \rightarrow X\)
dropout 正则化后加上残差 \(\large X \leftarrow dropout(X) + R\),再记录残差 \(\large R \leftarrow X\)
输入到第三子层中
最后一层输出后,通过线性层映射出去 \(\large W^TX \rightarrow X \in \mathbb{R}^{B \times T' \times V'}\)
计算softmax交叉熵,反向传播,更新梯度
2.3 Self-Attention
- \(\large d_k = d_v = D / h\),则query,key 和 value 分别对应的线性层为 \(W_q \in \mathbb{R}^{D \times (h\cdot d)}\),\(W_q \in \mathbb{R}^{D \times (h\cdot d)}\)
,\(W_q \in \mathbb{R}^{D \times (h\cdot d)}\)
三个输入参数分别经过线性层后,并把维度转换为 \(\large Q, K, V \in \mathbb{R}^{B \times h \times T \times d}\)
矩阵乘法得到相似性得分矩阵 \(\large (s \cdot Q) * K \rightarrow A \in \mathbb{R}^{B \times h \times T' \times T}\),其中 \(\large s=1/\sqrt{d}\)
遮罩计算,\(\large A \leftarrow masked(A)\)。对于encoder的第一个子层和decoder的第二个子层,把源句子中的边缘位置得分设为负无穷,对于decoder的第一个子层,我们还需要把每一个位置的后面位置的得分设为负无穷。
计算softmax得到归一化的相似性矩阵,\(\large A \leftarrow softmax(A)\),正则化 \(\large A \leftarrow dropout(A)\)
通过矩阵乘法与 value 加权求和,求得注意力得分 \(\large A * V \rightarrow X \in \mathbb{R}^{B \times h \times T \times d}\)
连接 \(\large h\) 个head \(\large X \in \mathbb{R}^{B \times T \times D}\)
经过一个线性层后输出 \(\large W^TX \rightarrow X \in \mathbb{R}^{B \times T \times D}\)
前面提到我们在计算decoder第一子层的注意力时把每一个位置的后面位置的得分设为负无穷,目的是防止未来无用信息的干扰。我们构造该句子的方法是在去边缘的遮罩矩阵基础上,取该矩阵的上三角矩阵,即把相似性矩阵的边缘位置和上三角位置都设为负无穷。
2.4 Feed-Forward Network
构造两个线性层,\(\large W_1 \in \mathbb{R}^{D \times F}\) 和 \(\large W_2 \in \mathbb{R}^{F \times D}\) 。
记录残差 \(\large R \leftarrow X \in \mathbb{R}^{B \times T' \times D}\),标准化 \(\large X \leftarrow Norm(X)\)
通过第一个线性层并使用ReLU激活函数 \(\large ReLu(W_1^TX) \rightarrow X \in \mathbb{R}^{B \times T' \times F}\)
正则化后在通过第二个线性层 \(\large W_2^T(dropout(X)) \rightarrow X \in \mathbb{R}^{B \times T' \times D}\)
加上残差后输出 \(\large X \leftarrow X + R\)
上述过程与论文不同的是,我们把标准化 Layer Normalization 移到注意力层的前面。这么做的原因在于当我不做改动时,模型预测结果很糟糕,结果全是 padding 或 eos,个人感觉是因为残差连接后再标准化会把残差丢失,详细原因也不是很肯定。而tensor2tensor中的建议也是放在前面的,既然如此,我就放在前面了。
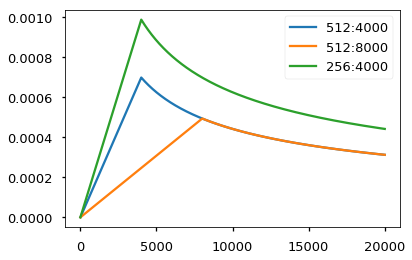
2.5 Optimizer
基于Adam,设 \(\large \beta_1 =0.9\),\(\large \beta_2=0.98\) 和 \(\large \epsilon = 10^{-9}\) ,热更新步为 \(\large w=4000\),在第 \(\large s\) 步时,则学习率更新规则为, \[ lr = D^{-0.5} \cdot min(s^{-0.5}, s \cdot w^{-1.5}) \] 学习率的变化如图所示,
4. 参数细节
- 词向量大小取 512
- head的数量为 8
- encoder和decoder都是 6 层
- 前馈传播网络的维度 \(\large F\) 为 2048
- dropout 为 0.1
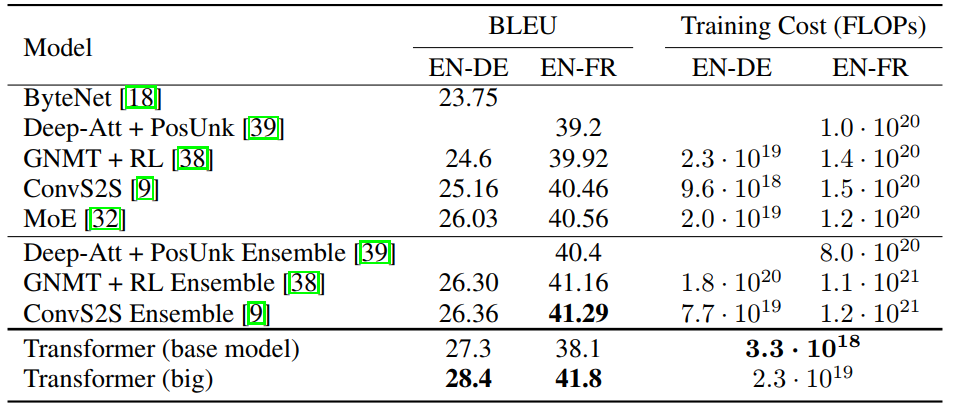
5. 结果
从论文中公示的结果来看,Transformer 模型得到了相当不错的结果,略胜 ConvS2S 一筹。
6. 自注意力的有效性
自注意力(self-Attention)主要特点是解决了远程依赖问题(long-range dependencies)。信号传递的距离越远,信号就变得越弱,远程依赖就越弱。RNN需要通过时间步的计算传递,信号传递长度是 \(\large \mathcal{O}(n)\),而自注意力是把整个序列的信号进行前一层和后一层的直接计算,所以只要 \(\large \mathcal{O}(1)\)。

Comments