Word2Vec模型中,主要有Skip-Gram和CBOW两种模型,从直观上理解,Skip-Gram是给定 Input Word 来预测上下文。而CBOW是给定上下文来预测。本篇文章仅讲解Skip-Gram模型。
数据获取
首先,每次都需要从语料库中抽样一个批次的数据,batch size 为 \(\large n\)
我采用窗口移动的方式获取,中心词(target)为 \(\large w_c\),窗口(Skip-window)为 \(\large m\),以中心词为中心,两扇窗口分别涵盖 \(\large m\) 个上下文词汇,则以中心词为中心的取词跨度(span)是 \(\large 2 * m + 1\)。
\[ w_{c-m}, \,.. \, ,w_{c-1}, w_{c}, w_{c+1}, \, .. \,, w_{c+m} \]
有一个参数是取词数量(num-skips),表示每次移动窗口取多少个上下文词汇。以上面为例,假设num-skips为2,那么可能取到的数据是 \(\large w_c \rightarrow w_{c+m},\; w_c \rightarrow w_{c+1}\),没有规定分别取前后多少词,每次在跨度内除中心词外随机取。
中心词每向后移动一次,则重复上面的操作,直到取满批次大小,最少移动 \(\large n/\text{num-skips}\) 次。

算法
假设批次大小是 \(\large n\),Skip-gram的目标函数为:
\[ \mathcal{L}_{SG}=-\frac{1}{n}\sum_{i=1}^n\sum_{|j|\le c} log\;p(w_{i+j}|w_i) \]
概率函数 \(\large p\) 是我们重点讨论的对象。 我们使用两个词向量去拟合,假设词向量的的维度是 \(\large E\),词汇表有 \(\large V\) 个单词。
- \(\large w_i\): 词汇表第 \(\large i\) 个单词
- \(\large V \in \mathbb{R}^{V \times E}\): 输入词向量
- \(\large v_i\): \(\large V\)的第 \(\large i\) 行,单词 \(\large w_i\) 的输入向量表示
- \(\large U \in \mathbb{R}^{V \times E}\): 输出词词向量
- \(\large u_i\): \(\large U\)的的第 \(\large i\) 行,单词 \(\large w_i\) 的输出向量表示
中心词的词向量由输入词向量获得,上下文词的词向量由输出词向量获得。中心词 \(\large c\) 与之对应的上下文词汇 \(\large w\) 的词向量的乘积再求和就该中心词的得分 \(\large z_c^w = \sum^E_i u_w^i v_c^i\)。
以前会使用softmax函数,但总所周知,softmax函数的计算代价是昂贵的。所以论文作者提出了负采样( negative samples),称为负采样Skip-gram(SGNS)。
假设单词在上下文中,我们称为正样本 \(\large w \in D^+\),若单词不在上下文中,我们称为负样本 \(\large \hat w \in D^-\)。每计算一个正样本会携带计算 \(\large K\) 个负样本, 这个 \(\large K\) 不会很大,一般5~20个,数据集越大,这个值越小。
我们要最大化,下面这个函数
\[ \begin{aligned} & z_c^w = \sum^E_i u_w^i v_c^i \\ & \hat z_c^{\hat w} = \sum^E_i u_{\hat w}^i v_c^i \\ & \max_{U,V}\;log\;\sigma(z_c^w)+\sum_{(\hat w_k,c)\in D^-}^K log\;\sigma(-\hat z_c^{\hat w_k}) \end{aligned} \] 即尽量使得正采样的得分变大,而负采样的得分变小。
那么我们可以得到目标函数为,
\[ J = -\frac{1}{n}\sum_{i=1}^n \Big(log\;\sigma(z_{c_i}^{w_i})+\sum_{(\hat w_k,c_i)\in D^-}^K log\;\sigma(\hat z_{c_i}^{\hat w_k})\Big) \]
然后使用随机梯度下降最小化目标函数即可。Kaji, et al. (2017) 建议最好使用原生的随机梯度下降,学习率 \(\large \alpha\) 为1.0,不需要使用Adam或AdaGrad。实验发现,使用Adam或AdaGrad等得到的效果不如SGD,而且还会降低计算效率。
一般的,我们会以输入向量 \(\large V\) 作为最终的词向量。
噪音分布(noise distribution)
负样本的选取并不是完全随机的,其中定义了一个噪声分布去选取负样本 [1]。 我们定义一元组分布(unigram distribution)为单个单词数量与总单词数量的比值的概率分布,即
\[ U(w_i) = \frac{count(w_i)}{\sum_i count(w_i)} \]
而噪声分布定义为
\[ P_n(w_i) = \frac{U(w_i)^{\frac{3}{4}}}{Z} \]
其中 \(\large Z\) 是一个扩大系数,一般为 \(\text{0.001}\)。 噪音分布的用意是使频繁出现的词更容易被选为负样本,而不频繁出现的词不作为负样本。为什么呢?比如说,类似于\(\text{is, a, the}\) 这样的高频词,他们没有实际意义,而且不是我们所关心的,所以应该更多的把他们作为负样本。
为什么要选择\(\large \frac{3}{4}\) 次幂呢?在google输入plot y = x^(3/4) and y = x,可以看到曲线的变化趋势
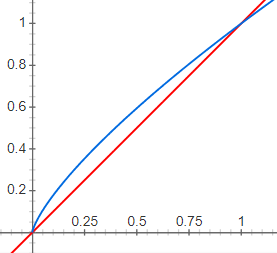
其中蓝色曲线是\(\large \frac{3}{4}\) 次幂的,越接近1,增量就越小,目的是适当减少超高频词数量。
\(\large P_n(w_i)\) 在实际使用中就是词汇 \(\large w_i\) 在总负样本池中出现的次数。
代码实现
我用pytorch实现了SGNS算法,详见Github
测试
经过测试使用了噪音分布后,负样本池的大小减少了非常多,而且 spearmans_rho 得分也提高了一点。
| eval-data | use-noise | non-noise |
|---|---|---|
| EN-MC-30 | 0.2513 | 0.2405 |
| EN-MTurk-287 | 0.2578 | 0.2357 |
(词向量300d,训练20万步)

Comments