循环神经机器翻译

2018-12-31 NLP,机器学习,深度学习

编码和解码

我们把源句子（source sentence）表示为 \(\large (x_1, x_2, \dots, x_n) \in x\), 目标句子（target sentence）表示为 \(\large (y_1, y_2, \dots, y_n) \in y\)。

使用编码网路（encoder）对源句子进行编码，使用解码网络（decoder）对源句子的编码进行解码，解码出预测句子。同时，作为监督，把目标句子作为解码网络的输入。

本文主要讲使用循环神经网络构建encoder-decoder模型。

源句子的最大序列长度为 \(\large T\), 目标句子的最大序列长度为 \(\large T'\)，批次大小为 \(\large B\)，词向量大小为 \(\large E\)，RNN的隐藏层大小为 \(\large H\), 源语言词汇数量为 \(\large V\)，目标语言词汇数量为 \(\large V'\)。

  1. 一个batch即一个句子，把句子填充到长度为 \(\large T\)， 依次输入一个词，经过词向量 \(\large X \in \mathbb{R}^{T \times B \times E}\)。
  2. encoder 一次性输入整个源句子 \(\large X\) 和隐藏状态 \(\large h \in \mathbb{R}^{T \times B \times H}\)
  3. encoder 输出 \(\large X \in \mathbb{R}^{T \times B \times H}\) 和 \(\large h \in \mathbb{R}^{T \times B \times H}\)
  4. decoder 把时间步拆开，每一时间步的输入为上一时间步的隐藏状态和预测词，除了预测词，也可以用目标句子中的词，一个时间步输入数据为 \(\large X_i \in \mathbb{R}^{1 \times B \times E}\) 和上一时间步的隐藏状态 \(\large h \in \mathbb{R}^{1 \times B \times H}\)
  5. decoder 一个时间步的输出为 $O ^{1 B H} $ 和隐藏状态 \(\large h\)。然后再下一个词向量 \(\large X\) 和 \(\large h\) 输入到下一时间步，执行第4步，直到句子末尾。
  6. 我们把decoder每一时间步的输出收集起来 \(\large Y \in \mathbb{R}^{T' \times B \times E}\)
  7. decoder的输出要用于softmax函数，所以每一时间步的输出通过一个线性层 $W ^{H V'} $，则最后的输出 $Y ^{T' B V'} $
  8. 为了方便计算，把decoder的输出压缩成二维 $Y ^{(T' * B) V'} $ ，并使用softmax交叉熵计算损失值
  9. 反向传播并梯度更新

seq2seq网络结构如图所示：

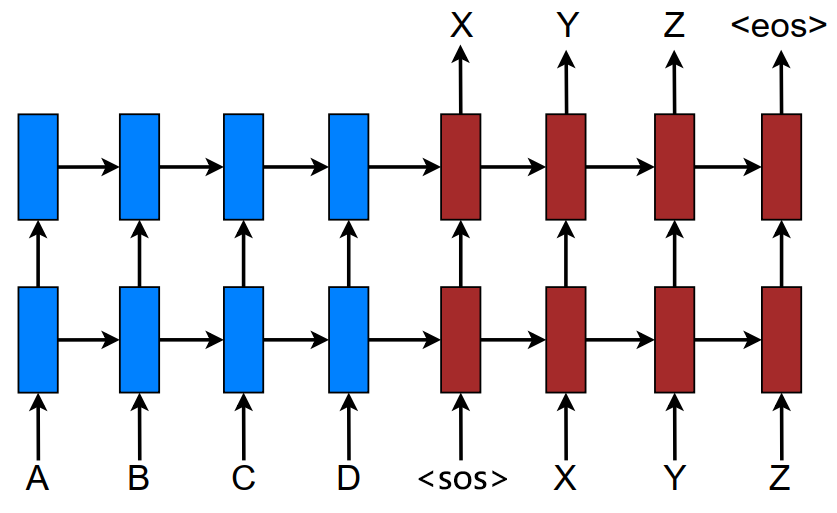
因为我们是按批次计算，一个批次中的句子有长有短，为了统一长度，会对所有句子填充 \(\large \langle pad \rangle\)。而句子尾部会填充 \(\large \langle eos \rangle\) 表示结束，目标句子会在句首加一个\(\large \langle sos \rangle\)，通过这个起始标志输出第一个词汇。

目标句子包含 \(\large \langle eos \rangle\) , \(\large \langle sos \rangle\) 和 \(\large \langle pad \rangle\) 的序列长度是 \(\large T'\)，

\[ \large \langle sos \rangle, I, love, you,\large \langle eos \rangle, \large \langle pad \rangle, \dots, \large \langle pad \rangle \]

但因为decoder以 \(\large \langle sos \rangle\) 为起点，预测输出的是不包含 \(\large \langle sos \rangle\) 的，所以计算交叉熵时目标句子应该去掉 \(\large \langle sos \rangle\) ，长度变为 \(\large T'-1\)， 但是decoder输出长度为 \(\large T'\)，长度不一致。这时注意到，句子末尾是一堆无意义的 \(\large \langle pad \rangle\) ，预测出来的同样是无意义的，所以我们可以把decoder输入的最后一个去掉，这样序列长度就一致了。

注意力机制（Attention Mechanism）

注意力机制有两个作用：

其一，是区分哪部分是重要的。当你听到句子“the ball is on the field”，你不会认为这 6 个单词都一样重要。你首先会注意到单词“ball”，“on” 和 “field”，因为这些单词你是觉得最“重要”的。类似，Bahdanau 等人注意到使用 RNN 的最终状态作为 Seq2Seq 模型的单个“上下文向量”的缺点：一般对于输入的不同部分具有不同的重要程度。再者，此外，输出的不同部分甚至可以考虑输入的不同部分“重要”。

其二，是具有更长时间的记忆力。你会注意到，当你通过编码网络输出特征向量后，解码阶段就只是根据这个向量来解码，而不再有其他信息。如果我们可以持续从编码网络获取信息，那么我们的预测不是更准确一些吗？就好像人类翻译员，他们肯定也不是只看一眼原句，就能翻译出来，而是对照着原句一个一个翻译。

注意力机制的基本方法就是在解码阶段获取编码阶段的信息。

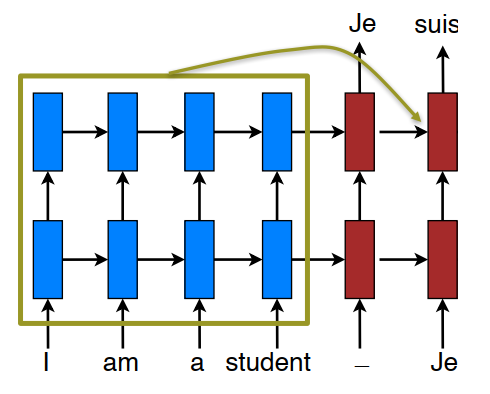
全局注意力（Global Attention）

所谓全局注意力，即把encoder的所有输出的信息参加到decoder每一时间步的输出的计算中。简单的说就是，当我们预测每一个词时，我们会参考源句子中每一个词，每个源词汇都会得到一个注意力得分（score）。

为了计算注意力，我们把decoder的每一时间步拆开计算。

假设当前时间步的输出为 \(\large y \in \mathbb{R}^{1 \times B \times H}\)，而encoder的输出为 $O ^{T B H} $。则得分函数可以有以下三种，

\[ score(y, O) = \begin{cases} y^TO \\ (y^TW)^TO \\ v^T tanh(W[y;O]) \end{cases} \]

（一般用第二种）

为了得到得分矩阵，我们计算时会进行转置，\(\large y \in \mathbb{R}^{B \times 1 \times H}\)， $O ^{B H T} $，矩阵相乘后得到注意力得分 \(\large a \in \mathbb{R}^{B \times 1 \times T}\)，一般我们还会对它用softmax计算。

  1. 我们需要得到一个上下文向量 \(\large a \times O \rightarrow context \in \mathbb{R}^{B \times 1 \times H}\)
  2. 把上下文向量与decoder时间步的输出相连，并经过线性层输出注意力向量 \(\large concat(context, y)^T W \rightarrow attn \in \mathbb{R}^{B \times 1 \times H}\)
  3. 把中间维度去掉后，经过线性层输出 $y ^{B V'} $
  4. 当decoder的 \(\large T'\) 个时间步算完后，我们就能完整的输出序列 \(\large Y \in \mathbb{R}^{T' \times B \times V'}\) ，以及所有的注意力得分 \(\large a\) 组成了对齐矩阵（alignment matrix）\(\large align \in \mathbb{R}^{B \times T' \times T}\)

对齐矩阵如图所示：

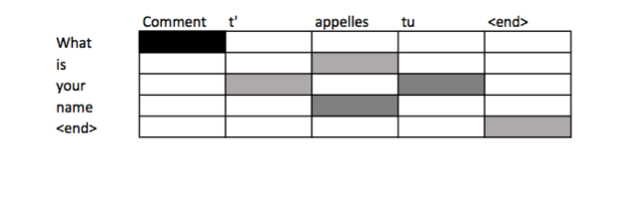
这个表是将源句子中的单词映射到目标句子中的相应单词，越深色表示相关性越大。

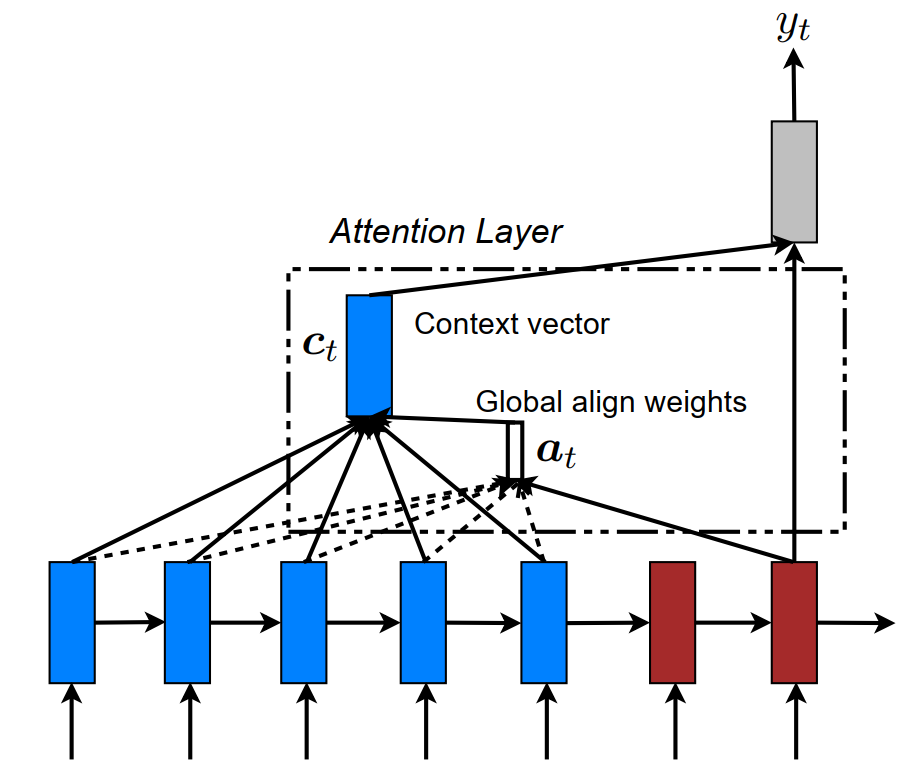
全局注意力网络结构：

Input-Feeding

Luong et al. (2015) 中提出了Input-Feeding模型 [1]，将注意力向量 \(\large attn\) 和目标词向量连接后作为decoder RNN的输入，即每一时间步的输入为 \(\large y \in \mathbb{R}^{B \times 1 \times (E+H)}\)。

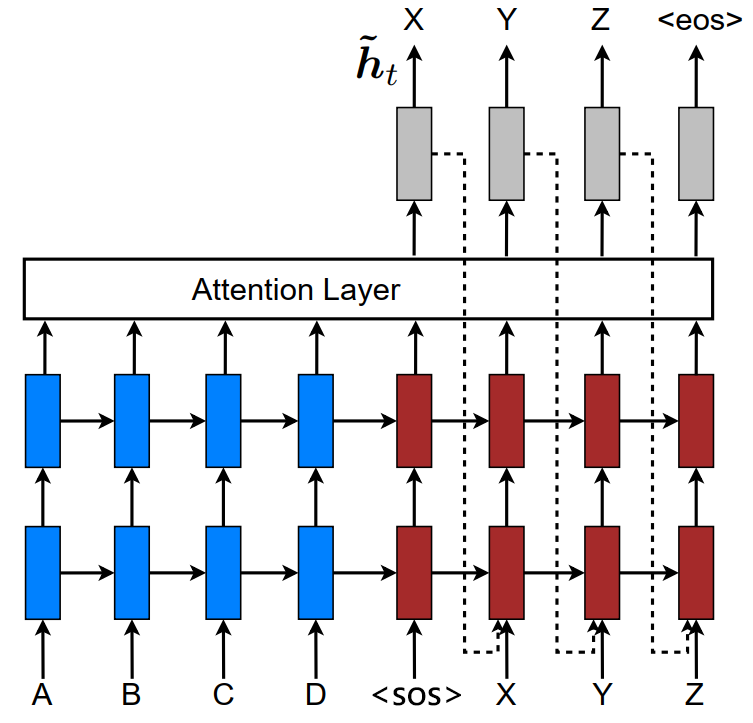
Teacher Forcing

所谓Teacher Forcing就是对每一时间步的输入使用目标句子中正确的词汇，而不是上一时间步输出的预测词。

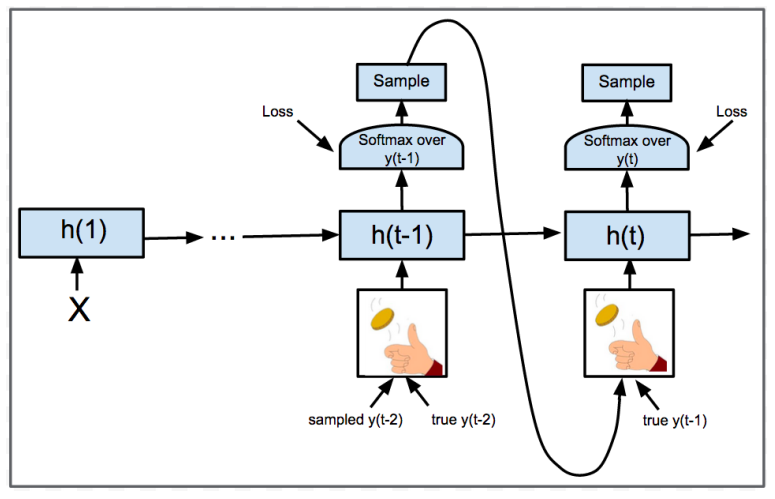
Scheduled Sampling

Scheduled Sampling 直译“计划抽样” [2]，是介于Teacher Forcing和Without Teacher Forcing之间的方法。我们设置一个使用Teacher Forcing的概率分布，对于每一时间步，我们使用该概率分布来绝对是否使用Teacher Forcing。若使用，我们就输入目标句子中的词汇，否则输入上一时间步的预测词。

论文中的方案是每一时间步就抛硬币选择一次，但实际训练中为了统一，一般是一个batch选择一次。

评估

我们对机器翻译的评估通常会用BLEU算法 [3]。它是一种比较参考翻译（Reference），即人工翻译，与机器翻译的得分算法。

我们对参考句子和预测句子取n元组（n-grams）, 机器翻译结果为 \(\large \hat y\), 得分为：

\[ P_n = \frac{\sum_{ngrams \in \hat y}Count_{ref}(ngrams)}{\sum_{ngrams \in \hat y}Count_{MT}(ngrams)} \]

而BLEU得分的定义为，我们将1至n元组的得分求和再求均值，然后用指数函数放大，

\[ BLEU = \beta \; exp({\frac{1}{n}\sum_{i=1}^n P_i}) \]

其中 \(\large \beta\) 是惩罚因子, 也叫简短惩罚（brevity penalty）。如果你输出了一个非常短的翻译，那么它会更容易得到一个高精确度。因为输出的大部分词可能都出现在参考之中，这时就要对得分进行惩罚。

假设，参考翻译的长度为 \(\large r\), 若有多个句子就取平均值。机器翻译句子长度为 \(\large m\)。

\[ \beta = \begin{cases} 1 & if \, m > r \\ exp(1-\frac{r}{m}) & otherwise \end{cases} \]

如果机器翻译句子大于参考翻译句子长度，我们就不进行惩罚；若小于，\(\large 1-\frac{r}{m}\) 为负数, 而指数函数会得到一个小数，使得bleu得分降低。

你也许会直觉的认为，解码器就是直接将每个时间步的输出通过softmax找到最可能的那个词汇即可，这也叫贪心查找（Greedy Search）。但在这只是考虑到一个词的最优选择，而不是整体最优选择。

如图，一句话可能会有成多种翻译版本

如果按照局部最优的选择，那可能会输出第一句。如果按照整体最优，那可能是第三句。而实际上，我们应该考虑整体最优。

\[ \mathop{argmax}_{y_1,y_2,...,y_T}\,P(y_1,y_2,...,y_T|x) \]

目前比较好的方法是束搜索（Beam search）[4]。

定义一个束宽 \(\large b\)，每个序列得分函数为 \(\large F(w)\)。

  1. 第一个时间步输出时，我们会从词汇表 \(\large V\) 中找 \(\large b\) 个得分 \(\large F(w)\) 最大的词汇，加入到对应的序列当中。假设 \(\large b = 3\)，那么就有3个候选序列 \(\large s_1(w_1), s_2(w_2), s_3(w_3)\)

  2. 对于第一个时间步的每一个候选，依次输入到第二个时间步中，找得分最大的 \(\large b\) 个词汇分别加入到该候选序列中，由一个候选序列变成 \(\large b​\) 个候选序列

\[ s(w_1,w_4), s(w_1, w_5), s(w_1, w_6) \]

总共可以得到 \(\large b^2\) 个候选序列 \(\large s_1^1, s_1^2, s_1^3, s_2^1, s_2^2, \dots\) 。假设序列长度为 \(\large L\) ，一个序列的总得分为每个词的得分之和 $F(s) = _i^ L F(w_i) $，则该序列的平均得分为 \(\large score = F(s) / L\)。我们保留 \(\large b\) 个平均得分最高的序列，进入下一时间步。

  1. 往后重复类似于第2步的操作，当其中一个序列的最后一个词为 \(\large \langle eos \rangle\) 时，该序列就停止搜索，直到所有序列都停止或者到达指定的最大长度为止。

  2. 最后从 \(\large b\) 个序列选取平均得分最高的序列。

对于得分函数，我们一般使用

\[ F=log(softmax(Y)) \]

束搜索一般用在测试阶段。

卷积机器翻译

使用循环神经网络训练的感觉就是慢。使用卷积网络进行机器翻译可以实现并行化，大大提高训练效率。这部分我打算放到另一篇文章中讲。

参考文献

#NLP #深度学习 #机器学习
卷积序列模型 GloVe

Comments

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×