Red black tree implementation

2020-08-02 算法设计

Red black tree is a data structure for searching data and can self-balance after modification. I will try to implement it and log in this article. You can find the source code in here.

Node

Evey Node have five member properties. color_ represent the color of node, red or black. 

1
2
3
4
5
6
7
8
9
10
11
12
enum RbTreeColor { rb_red = false, rb_black = true };

template <typename T>
struct RBNode {
    typedef RBNode<T>* SelfPtr;
    typedef const RBNode<T>* ConstSelfPtr;

    RbTreeColor color_;
    SelfPtr parent_;
    SelfPtr left_;
    SelfPtr right_;
    T value_;

Iterator

function increment() find the last node that is larger than current node, corresponding operator++. function decrement() find the last node that is smaller than current node, corresponding operator--. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
template <typename T, typename Ref, typename Ptr>
struct RBTreeIterator {
    // ...

    typedef RBTreeIterator<T, Ref, Ptr> Self;
    typedef RBNode<T>* NodePtr;

    NodePtr node_;

    explicit RBTreeIterator() = default;
    explicit RBTreeIterator(NodePtr x): node_(x) {}

    void increment() {
        if(node_->right_ != 0) {
            node_ = node_->right_;
            while(node_->left_ != 0) {
                node_ = node_->left_;
            }
        } else {
            NodePtr y = node_->parent_;
            while (node_ == y->right_) {
                node_ = y;
                y = y->parent_;
            }
            if(node_->right_ != y) {
                node_ = y;
            }
        }
    }

    void decrement() {
        if(node_->color_ == rb_red && node_->parent_->parent_ == node_) {
            node_ = node_->right_;
        } else if (node_->left_ != 0) {
            NodePtr y = node_->left_;
            while (y->right_ != 0){
                y = y->right_;
            }
            node_ = y;
        } else {
            NodePtr y = node_->parent_;
            while (node_ == y->left_) {
                node_ = y;
                y = y->parent_;
            }
            node_ = y;
        }
    }

    reference operator*() const { return node_->value_; }
    pointer operator->() const { return &(node_->value_); }
    Self& operator++() {
        increment();
        return *this;
    }
    Self& operator--() {
        decrement();
        return *this;
    }

    // ...

Tree Property

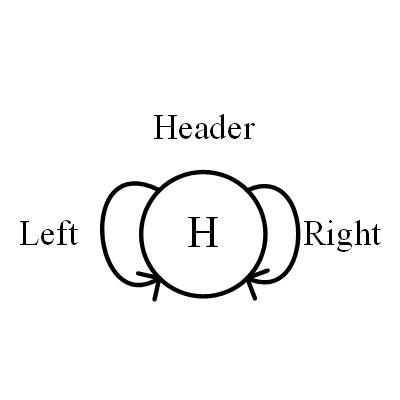
rb-1.jpg
rb-1.jpg
  • parent: link to root if exist
  • left: also call leftmost, link to the most left node of tree
  • right: also call leftmost, link to the most right node of tree
  • color: default is red

root

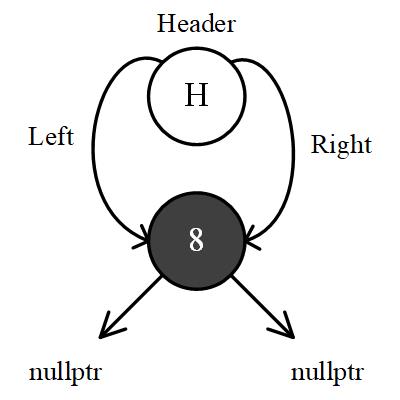
rb-2.jpg
rb-2.jpg
  • parent: link to header
  • left: link to nullptr if no node
  • right: link to nullptr if no node
  • color: always is black

Multi Node

See a tree with multi nodes. The children of leaf are nullptr.

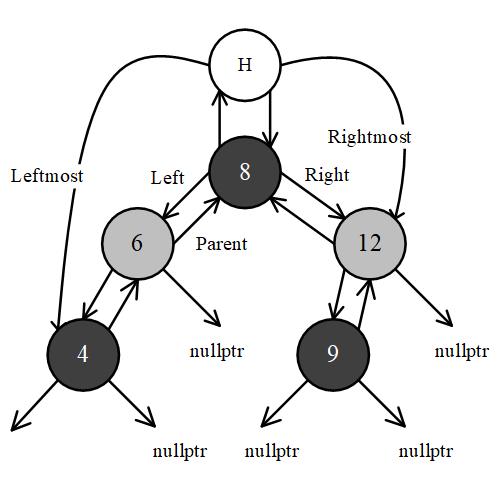
rb-3.jpg
rb-3.jpg

Rotation

Left Rotation

When the right sub-tree is taller, we need to rotate left to shorten it. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
 *        x              y
 *       / \            / \
 *      u   y    =>    x   b
 *         / \        / \
 *        a   b      u   a
 *
 */
inline void _rotate_left(NodePtr x, NodePtr& root) {
    NodePtr y = x->right_;
    x->right_ = y->left_;
    if(y->left_ != 0) {
        y->left_->parent_ = x;
    }
    y->parent_ = x->parent_;

    if(x == root) {
        root = y;
    } else if(x->parent_->right_ == x) {
        x->parent_->right_ = y;
    } else {
        x->parent_->left_ = y;
    }
    y->left_ = x;
    x->parent_ = y;
}

Right Rotation

When the left sub-tree is taller, we need to rotate right to shorten it. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
 *         x             y
 *        / \           / \
 *       y   u    =>   a   x
 *      / \               / \
 *     a   b             b   u
 */
inline void _rotate_right(NodePtr x, NodePtr& root) {
    NodePtr y = x->left_;
    x->left_ = y->right_;
    if(y->right_ != 0) {
        y->right_->parent_ = x;
    }
    y->parent_ = x->parent_;

    if(x == root) {
        root = y;
    } else if(x->parent_->right_ == x) {
        x->parent_->right_ = y;
    } else {
        x->parent_->left_ = y;
    }
    y->right_ = x;
    x->parent_ = y;
}

Rule and Balance

  1. The color of node is eithor red or black.
  2. The root node always is black.
  3. If a node is red, its children must be black.
  4. Every path of every sub-tree have the same number of black nodes.

As the rule 4, we can ensure the different of the height of the tallest sub-tree and that of the shortest sub-tree cannot over 2 times. The color is the measure of the balance for red black tree, as the height difference for the AVL tree.

Insertion

We insert a not-allow-replaced key with three considerations:

  1. insert to the left of leftmost
  2. insert to the right of y if just bigger than y
  3. insert to the left of y if just bigger than decrement(y)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
pair<iterator, bool> insertUnique(const Val &v) {
    NodePtr y = header_;
    NodePtr x = root();
    bool comp = true;
    while(x != nullptr) {
        y = x;
        comp = keyCompare_(KeyOfValue()(v), key(x));
        x = comp ? left(x) : right(x);
    }
    // while end, y will be the parent of the node to insert

    iterator j = iterator(y);
    if (comp) { // comp is true, insert to left
        if (j == begin()) {
            return pair<iterator, bool>(_insert(x, y, v), true);
        } else { // if j is not the leftmost
            --j;
            // need to --j, because KeyOfValue(v) probably equal to --j,
            // it need to be bigger than --j as the following comparsion.
        }
    }

    if (keyCompare_(key(j.node_), KeyOfValue()(v))) {
        return pair<iterator, bool>(_insert(x, y, v), true);
    }
    return pair<iterator, bool>(j, false);
}

// x is the position need to be inserted
// y is the parent of x
// v is the new value
iterator _insert(NodePtr x, NodePtr y, const Val& v) {
    NodePtr z;

    if(y == header_
    || x != nullptr
    || keyCompare_(KeyOfValue()(v), key(y))) { // insert to left of y
        z = createNode(v);
        left(y) = z;
        if(y == header_) {
            root() = z;
            rightmost() = z;
        } else if (y == leftmost()) {
            leftmost() = z;
        }
    } else {
        z = createNode(v);
        right(y) = z;
        if(y == rightmost()) {
            rightmost() = z;
        }
    }
    parent(z) = y;
    left(z) = nullptr;
    right(z) = nullptr;

    // rebalance the tree
    _rebalance(z, root());
    ++nodeCount_;
    return iterator(z);
}

Inside and Outside

For convenient, we define the inside and outside as shown blow. If the cur node direction is not equal to the parent direction, we call it inside, or else we call it outside.

1
2
3
4
5
6
7
8
9
10
11
12
13
/*
 *         v
 *        / \
 *       a   u
 *      / \           a is a left node
 *     b   c          b is outside, c is inside
 *    
 *        v
 *       / \
 *      u   a
 *         / \       a is a right node
 *        c   b      b is outside, c is inside
 */

ReBalance

Initially, x is new inserted node. x is red default. When its parent is red, which break the rule 3. If its parent is black, it do not breaks any rules, which does not need to rebalance.

You need to consider four situations: - First, we need to think about the parent of x is either a left or a right, which determines the rotation direction. - And then, consider the uncle of x is either red or black, which determines how to change the color.

In the process of percolation and rebalance, the parent of x initially is red, when percolate up, we change its color. How to change is determines to its sibling (uncle of x), which we need to make the color as same as its sibling.

  • If uncle is red, the grandparent must be black, all of you need to do is to change the color of parent and uncle to black, and grandparent's color to red, for following the rule 3. But these probably break the rules in higher position, so we need to percolate up to the grandparent.
  • After percolate up, if you find the parent is black, you can stop the rebalance, because the number of black have not changed and followed the rule 3 as above step. But if the parent is red, two continuous red node break the rule 3 again. And its uncle must be black or null. Looking at the following steps.
  • If uncle is black or null,
    • If cur node is in outside, change parent's color to black and grandpa's color to red. These will make the number of black nodes in its parent sub-tree increase 1 and greater than that of the uncle sub-tree, so we do a rotation to make the parent move to the grandpa position to make anthor direction sub-tree have the same number of black nodes. The rotation direction is opposite to its direction to its parent.
    • If cur node is in inside, we need to do a rotate firstly (the rotation direction is same to its direction to its parent) to make the cur node becomes the parent node, and the original parent node becomes the cur node in the outside, as same as the situation above, so do the same thing as above. (total two rotations)
  • Finally, making the root's color to black, these action do not break any rule.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
inline void _rebalance(NodePtr x, NodePtr& root) {
    x->color_ = rb_red;
    while(x != root && x->parent_->color_ == rb_red) {
        if(x->parent_ == x->parent_->parent_->left_) {  // parent is a left node
            NodePtr y = x->parent_->parent_->right_;    // consider uncle node
            if(y && y->color_ == rb_red) {  // uncle is red
                // parent and uncle change to black
                x->parent_->color_ = rb_black;
                y->color_ = rb_black;
                // grandparent change to red
                x->parent_->parent_->color_ = rb_red;
                x = x->parent_->parent_; // go up
            } else {    // uncle is black or is null
                if(x == x->parent_->right_) {   // x is inside
                    x = x->parent_;
                    _rotate_left(x, root); // rotate left
                }
                // parent's color become as same as uncle's
                x->parent_->color_ = rb_black;
                x->parent_->parent_->color_ = rb_red;
                _rotate_right(x->parent_->parent_, root); // rotate right
            }
        } else {    // parent is a right node
            NodePtr y = x->parent_->parent_->left_; // uncle
            if(y && y->color_ == rb_red) {  // uncle is red
                // parent and uncle change to black
                x->parent_->color_ = rb_black;
                y->color_ = rb_black;
                x->parent_->parent_->color_ = rb_red;
            } else {    // uncle is black or is null
                if(x == x->parent_->left_) {   // x is inside
                    x = x->parent_;
                    _rotate_right(x, root); // rotate left
                }
                x->parent_->color_ = rb_black;
                x->parent_->parent_->color_ = rb_red;
                _rotate_left(x->parent_->parent_, root);
            }
        }
    }
    // ensure root is black
    root->color_ = rb_black;
}

#算法设计
AVL Tree Implementation 无锁环形缓冲

Comments

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×