GloVe(Global Vector),是一种结合全局矩阵分解和本地上下文窗口的方法。LSA(latent semantic analysis)虽然能够有效的统计信息,但在词汇类比任务中表现很差。而Skip-gram虽然在词汇类比任务中表现很好,但依赖于窗口的移动,而不能有效统计全局的计数。论文作者认为,全局计数的对数加上双线性回归方法会非常合适。
算法
首先,我们需要对整个语料库建立一个统计全局词频的矩阵,一般称为共现矩阵(Co-ocurrence Matrix)。
假设,语料库有三句话:
- \(I \hspace{0.15cm} enjoy \hspace{0.15cm} flying\)
- \(I \hspace{0.15cm} like \hspace{0.15cm} NLP\)
- \(I \hspace{0.15cm} like \hspace{0.15cm} deep \hspace{0.15cm} learning\)
那他们的共现矩阵就是:
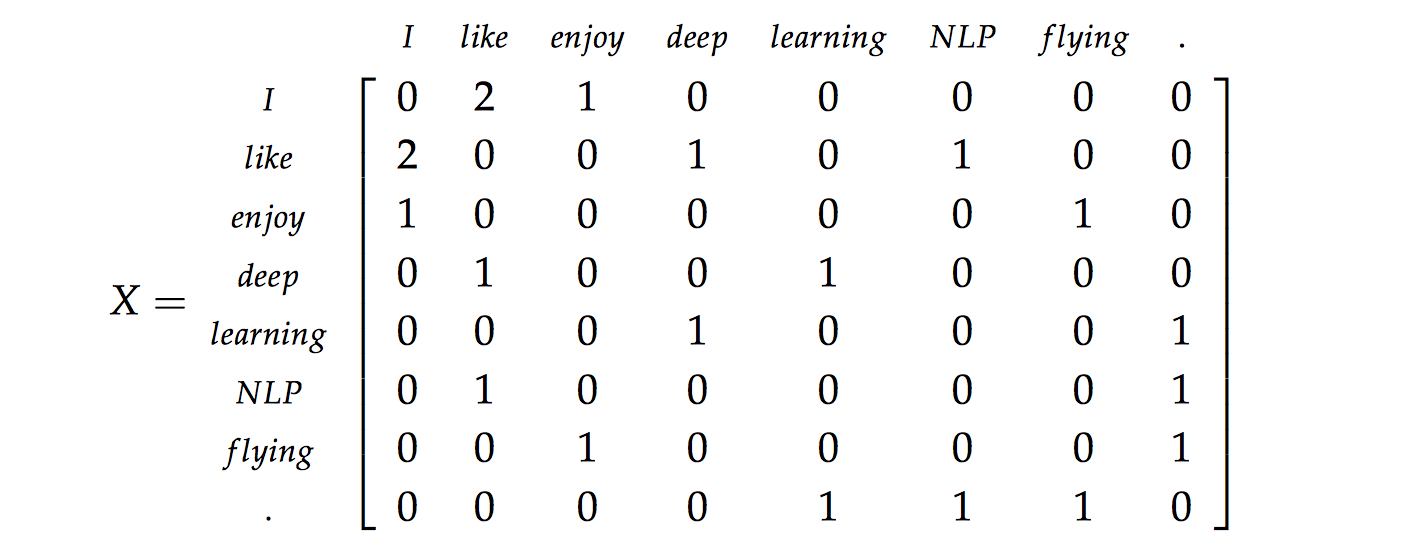
\(\large X_{ij}\) 表示单词 \(\large i\) 在单词 \(\large j\) 上下文出现的次数。你会发现,共现矩阵是对称的(symmetric),因为他同时取左右两边的单词,若只选取左边或右边的任一边,则是非对称的(asymmetric)。
构建词向量(Word Vector)和共现矩阵(Co-ocurrence Matrix)之间的近似关系,论文的作者提出以下的公式可以近似地表达两者之间的关系:
\[ u_i^Tv_j + b_i + \widetilde b_j \approx log(X_{ij}) \tag{1} \]
这里的 \(\large u_i, v_j\) 与Skip-Grams模型中的意义不同,它仅表示的是单词 \(\large i,j\) 之间的联系,没有中心与周围的区分。(对于公式(1),论文中做了相关推导,因为推导过程有些复杂,我把这部分放到文章后面。)
他的代价函数是:
\[ J = \sum_{i,j=1}^V f(X_{ij})(u_i^Tv_j + b_i + \widetilde b_j - log(X_{ij})) \]
其中 \(\large log(X_{ij}) \rightarrow log(1 + X_{ij})\),这么做的目的是防止出现 \(\large log0\) 的情况。 \(\large f(X_{ij})\) 是一个加权函数(weighting function),有些单词对经常同时出现,那么会导致 \(\large X_{ij}\) 会很大,应该衰减它们;而有些单词对从不一起出现,这些单词对就不应该对代价函数产生任何贡献,它们没必要去计算损失值,这时使用 \(\large f(0) = 0\) 来避免计算。
我们可以采用分段函数:
\[ f(x) = \begin{cases} (\frac{x}{x_{max}})^\alpha & if \; x < x_{max} \\ 1 & otherwise \end{cases} \]
函数图像如下:
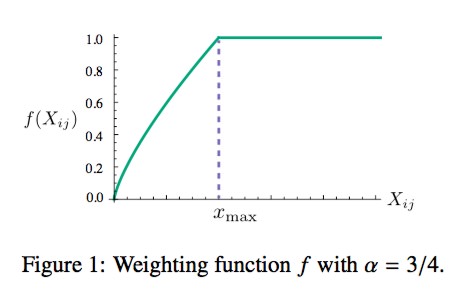
作者实验 \(\large \alpha\) 取值 0.75,\(\large x_{max}\) 取值 100。
\(\large u_i, v_j\) 的初始化可以不同,也可以相同。当训练得足够之后,\(\large u_i, v_j\) 与 \(\large X_{ij}\) 相似,而 \(\large X_{ij}\) 是对称的,所以 \(\large u_i, v_j\) 也是对称或接近对称。因为都是学习得到的参数,在我们看来没有本质区别。当初始化不同时,相当于加入了噪音,你可以选择把 \(\large e = u + v\) 作为最终向量,这样有助于提高鲁棒性。
实验结果
论文中展示了glove与word2vec等方法的对比,但其实大家都旗鼓相当。
下图是glove在不同参数的情况下的表现:
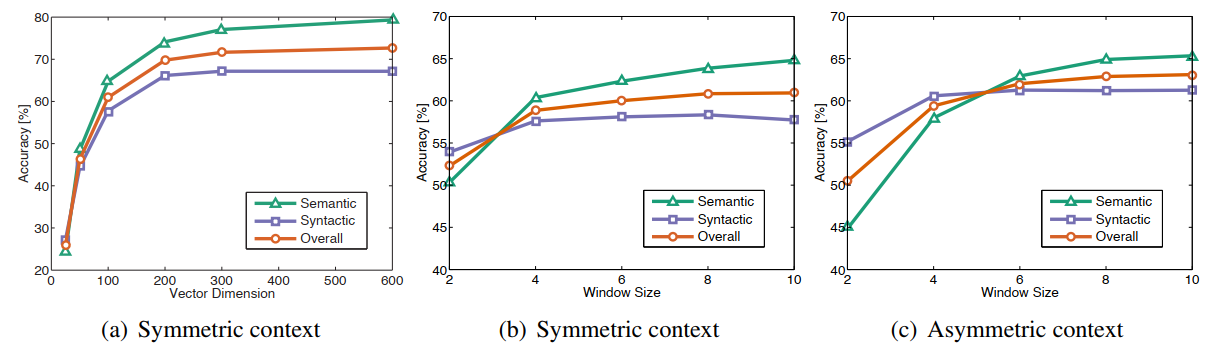
(图a 展示了向量维度对准确度的影响。图b和图c分别使用对称上下文和非对称上下文在不同窗口大小下的表现。以上所有测试都使用6B (billion) 的语料库)
可以发现最好的参数是300维度,窗口大小为5。再往上增加虽然能提高准确度,但也提高了计算代价,没有必要为了提升一点准确度而产生巨大的计算代价。
公式推导
这里对上面公式(1)进行推导。
论文中举了一个简单的例子:
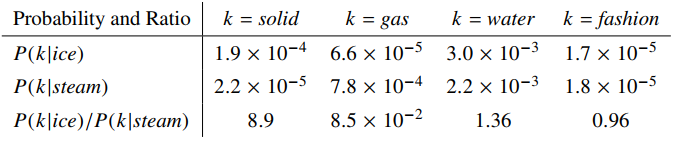
试问单词 \(\large k\) 应该是哪个单词?我们可以通过 \(\large P(k \vert ice)/P(k \vert stream)\) 来判断。当 \(\large P_{ik}/P_{jk}\) 很大的时候,说明 \(\large i\) 与 \(\large k\) 更接近一些。
然后,作者就想到,我们可以用参数去近似这个比值。
\[ F(w_i, w_j, w_k) = \frac{P_{ik}}{P_{jk}} \]
\(\large F\) 这里暂且设为未知函数,因为它包含了三个参数,所以我们需要削减一下参数,因为参数是线性的,所以自然可以构造成相减的形式。
\[ F(w_i - w_j, w_k) = \frac{P_{ik}}{P_{jk}} \]
然后我们用内积来表现两个单词向量的近似程度,
\[ F((w_i - w_j)^Tw_k) = \frac{F(w_i^Tw_k)}{F(w_j^Tw_k)} \]
提取其中一个单词的 \(\large F\),
\[ F(w_i^Tw_k) = P_{ik} = \frac{X_{ik}}{X_i} \]
我们设 \(\large F\) 为指数函数,则,
\[ w_i^Tw_k = log(P_{ik}) = log(X_{ik}) - log({X_i}) \]
然后,我们用偏置项来替代 \(\large log(X_i)\),即
\[ w_i^Tw_k + b_i + b_k = log(X_{ik}) \]
就这样,这个公式就被奇异地构造出来了。
代码实现
我自己用python实现了一下,但跑起来后发现这没什么意义。GloVe与Skip-gram不同,他构造共现矩阵需要花费大量时间和内存,这部分极度需要计算性能,用python跑半天都跑不完。 论文作者是使用纯C语言实现的,提供了不少预训练的模型,以及词向量的评估脚本,详见Github。

Comments