深度Q网络 (DQN)
回顾一下深度Q网络的过程。
- 从经验池 \(\large R\) 中获取 \(\large n\) 个转移,\(\large (s_i, a_i, r_{i+1}, t_i, s_{i+1})\),其中 \(\large t_i=1\) 表示 \(\large s_i\) 是结束状态
- 计算状态 \(\large s_i\) 的预测Q值,\(\large y_{pred}^i = Q(s_i)\),执行动作 \(\large a_i\) 时的值为 \(\large y_{pred}^{a_i}\)
- 计算状态 \(\large s_{i+1}\) 的目标Q值,\(y_{target}^i=Q'(s_i)\),取最优动作对应的值,即最大Q值 \(\large y_{target}^{max}\)
- 计算预期Q值 \(\large y_{expected}^i = r_{i+1} + (1-t_i) * \gamma * y_{target}^{max}\)
- \(\large n\) 个转移的均方差损失函数 \(\large loss=\frac{1}{n}\sum_i (y_{pred}^{a_i} - y_{expected}^i)\)
- 使用梯度下降最小化损失函数,更新 \(\large Q\) 网络的梯度值,注意这里不对目标网络 \(\large Q'\) 更新
- 相隔一定步数后,更新目标网络的参数 \(\large Q' = Q\)
其中,最重要的部分是对于期望Q值的计算,我们把这部分提取出来,
\[ Y_t^{DQN}=R_{t+1} + \gamma \max_{a} Q'(S_{t+1}, a; w^-) \]
使用经验池进行经验重新(experience replay)早在1992年就已经提出,而使用目标网络是在2015年由Mnih等人提出。
双深度Q网络(Double DQN)
不同于DQN,我们的期望Q值的计算为,
\[ Y_t^{DDQN} = R_{t+1} + \gamma \max_{a} Q'(S_{t+1}, \mathop{argmax}\limits_a Q(S_{t+1}, a; w); w^-) \]
我们的目标网络输入的不再是指定的 \(\large a\),而是原本的Q网络的最大Q值对应的动作。
深度Q网络的过度估计
论文中提出,DQN存在普遍的过度估计(overestimations)问题。
假设预测Q值为 \(\large Q_t(s, a)\),最优价值为 \(\large V_*(s)\) ,每个状态有 \(\large m\) 个动作,则平均误差为
\[ \frac{1}{m}\sum_a(Q_t(s, a) - V_*(s))^2 = C \]
从误差公式上看,环境的噪声,近似函数等因素都是Q函数参数学习的一部分,意味着任何这些因素都可能导致估值偏差。
对于最大值的估计,
\[ \max_aQ_t(s,a) - V_*(s) \ge \sqrt{\frac{C}{m+1}} \]
随着 \(\large m\) 的增大,下界越来越小,而实验结果的表现是随着 \(\large m\) 的增大,估计误差会越来越大,即 \(\large Q_t(s,a)\) 越来越大,产生了所谓的过分乐观(Overoptimism)。
过度乐观的实验
论文中选取的真值函数和近似函数分别为:
| True Value \(\large Q_*(s,a)\) | Approx Function \(\large Q_t(s,a)\) |
|---|---|
| \(\large sin(s)\) | \(\large W^TX\) (d=6) |
| \(\large 2exp(-s^2)\) | \(\large W^TX\) (d=6) |
| \(\large 2exp(-s^2)\) | \(\large W^TX\) (d=9) |
测试结果如下,其中每一行是一种真值函数,
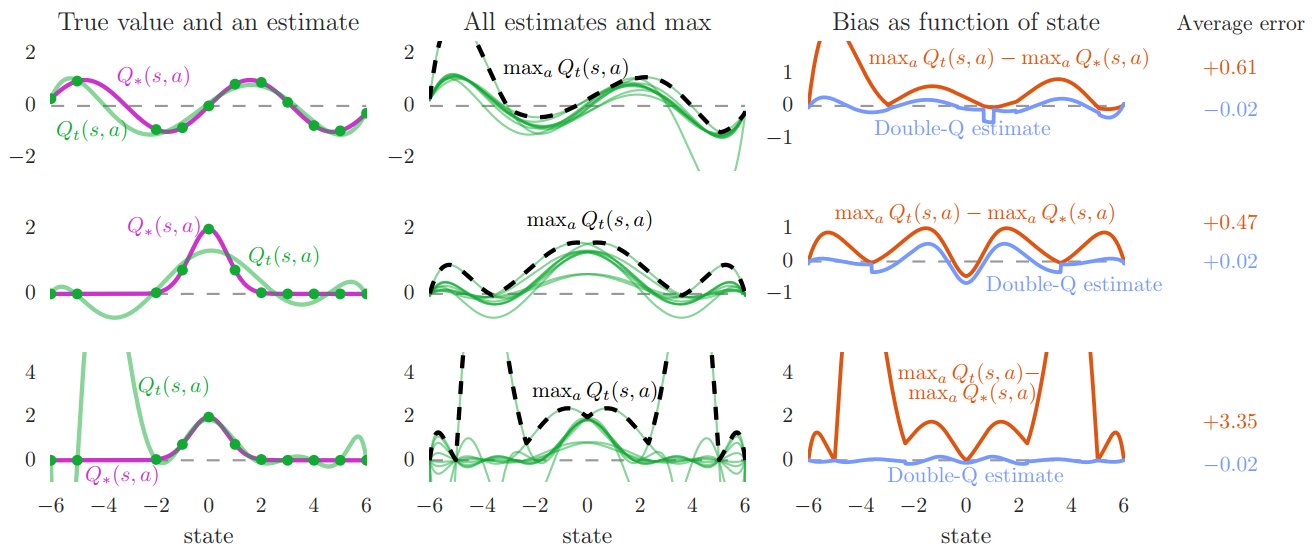
- 第一行第一幅图,描绘了其中一个动作,紫色是真值函数,绿色是拟合函数,可以看出6维的线性回归可以很好的拟合真值。
- 第一行第二幅图,描绘了10个动作的拟合函数随着的Q值曲线,用黑色描绘的是对应的最大Q值,你会发现最大值普遍大于真值。
- 第一行第三幅图,描绘了最大Q值与真值的误差,其中橙色曲线是DQN,蓝色曲线是DDQN。明显的,DQN的平均误差要远大于DDQN。
- 第三行第三幅图,你会发现9维的线性回归的拟合效果远不如6维(第二行第三幅图)。所以说明,有时候复杂的近似函数不一定取得好的效果。
实际效果
在atari游戏上运行对比。
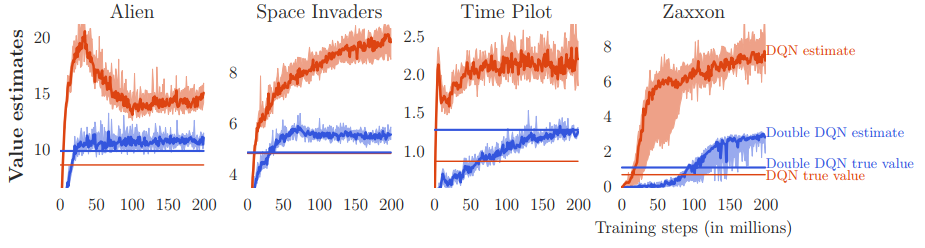
红色是DQN,蓝色是DDQN,其中横线表示无偏估计值。会发现DQN的估计值普遍大于DDQN,而且DQN的估计值偏离很严重。
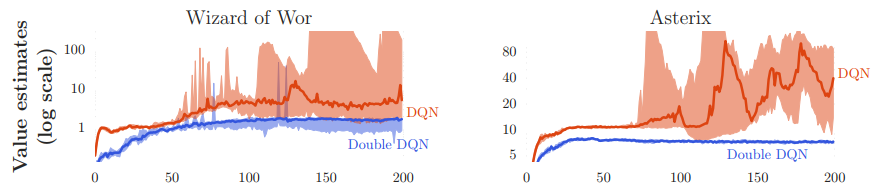
从上图发现,使用DQN的估计值(浅色区域)非常的不稳地,所以过高的估计值会影响学习效率。
总结
注意一个问题,上面我们一直都在讨论估计值的问题,DDQN能够降低估计值,使得他更接近真值。在实际训练中得到的好处就是训练过程不会太过动荡,也就提高了训练的效率。强化学习与深度学习不同,深度学习会设法得到一个高的准确度。而强化学习中无论是DQN还是DDQN,一直训练下去都能收敛到一个值上,算法的区别更多体现在训练的过程和效率上。
代码实现
我用pytorch分别实现了DQN,DDQN以及用DDQN算法运行atari游戏。详见Github。
测试结果
CartPole-v0
针对CartPole-v0问题,小车上面放着一个杆子,我们的任务是左右移动车子尽量使得杆子在车子上屹立得更久,每一步动作奖励为1,屹立时间越长得到的奖励越多,默认200步结束一个episode,gym认为一个最近100个episode的平均奖励大于195就认为解决。
我分别是用DQN和DDQN训练它,结果如下(蓝色是DQN,橙色是DDQN)
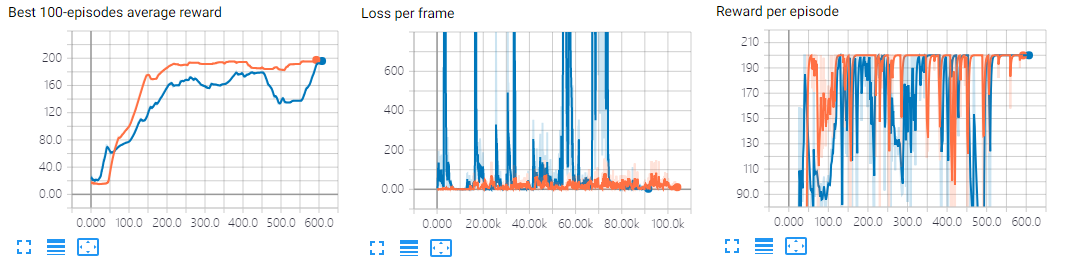
PongNoFrameskip-v4
Atari Pong 游戏就是两方在玩类似于乒乓球的游戏,当对方不能打回来,你就得分。目前,这是未解决问题,即没有一个奖励区间能说明解决该问题。
我用DDQN训练2百万帧,情况如下:
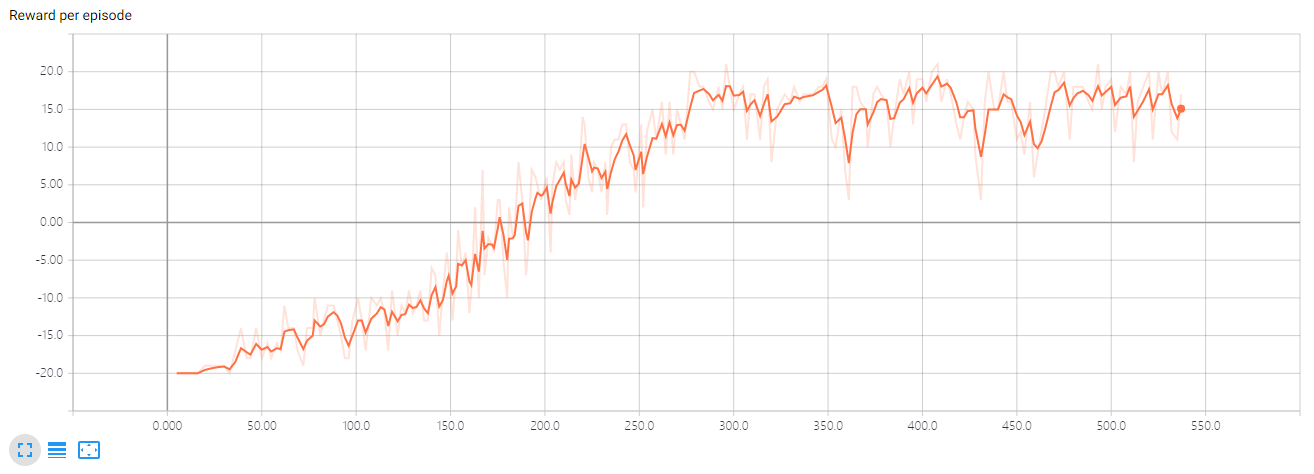
训练该环境时遇到了一些问题,一开始发现奖励曲线一直在-20左右徘徊,没有增长的趋势。后来我仔细对比了一下参数,发现Adam的学习率应该使用0.0001,而不是0.001。这也证明了调参的重要性,一个小数点就可能导致模型出现严重的偏差。

Comments