使用长短时期记忆(LSTM)用于序列模型取得了很好的效果,在2017年由Facebook提出了使用卷积神经网络构建Seq2Seq模型 [1]。循环神经网络通过窗口移动方式输入数据进行训练,当句子有 \(\large n\) 个窗口时,获得对应的特征表示的时间复杂度为 \(\large \mathcal{O}(n)\)。而使用卷积神经网络进行并行化计算,当卷积核宽度为 \(\large k\) ,其时间复杂度为 \(\large \mathcal{O}(\frac{n}{k})\)。
Encoder结构
我们采用一维卷积对序列进行处理,假设输入序列长度为 \(\large T\),卷积核宽度为 \(\large f\),边缘为 \(\large p\),则输出宽度为 \(\large T + 2p - f + 1\)。
源句子的最大序列长度为 \(\large T\), 目标句子的最大序列长度为 \(\large T'\),批次大小为 \(\large B\),词向量大小为 \(\large E\), 源语言词汇数量为 \(\large V\),目标语言词汇数量为 \(\large V'\),第一层卷积的通道数为 \(\large C\)。
整个句子的词向量为 \(\large X \leftarrow emb \in \mathbb{R}^{T \times B \times E}\)
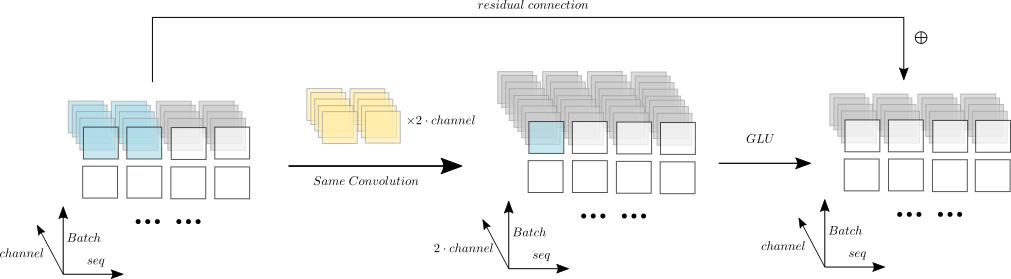
输入卷积层之前,要先通过一个线性层将维度规范到 $$\(\large X \in \mathbb{R}^{T \times B \times C}\),同时对维度做一个转置 \(\large X \in \mathbb{R}^{B \times C \times T}\)
卷积块带有残差结构 (residual),所以计算下一个卷积块之前保留一份残差 \(\large R \leftarrow X\)
在卷积计算时,我们不希望边缘向量产生影响,所以构造一个遮罩矩阵,将 \(\large \langle pad \rangle\) 位置值设为0,
\[ mask \in \mathbb{R}^{T \times B} \begin{cases} 0 & if \; x = pad \\ 1 & otherwise \end{cases} \]
转置和扩充维度 \(\large mask \in \mathbb{R}^{B \times C \times T}\),把边缘值的通道设为0,\(\large X \leftarrow X \circ mask\)
然后把 \(\large X\) 输入到一维卷积中 \(\large X \overset{conv}{\rightarrow} X \in \mathbb{R}^{B \times T \times 2C}\),这里指定输出通道是输入通道的2倍,而采用Same Convolution,所以序列长度不变
我们使用门控线性单元(Gated Linear Units)对卷积块的输出进行计算 [2],输出后通道数减半,
\[ \begin{align} & X \overset{split}{\rightarrow}A,B \in \mathbb{R}^{B \times C \times T} \\ & X = A \circ \sigma(B) \end{align} \]
加上残差,\(\large X \leftarrow X + R\);更新残差 \(\large R \leftarrow X\)
把 \(\large X\) 输入到下一卷积块,即下一层
从最后一个卷积块输出后,再经过线性层得到 \(\large O \in \mathbb{R}^{B \times T \times E}\)
除了 \(\large O\) 外,还要输出一个向量用于注意力计算 \(\large U \leftarrow O + emb^T\)
卷积块的计算过程如图所示:(图是我自己画的,如有错误请指出)
Decoder结构
Decdoer前面的结构基本与encoder一致,不同处有三个,
decoder的卷积层边缘 padding 设置为 kernel_size - 1。当输出时,我们去掉序列最后的 padding 个,以保持输入输出序列相同。这么做是为了确保当前信息不会受未来信息的影响
上述 (5) 计算完GLU后,还要输入到注意力层进行计算,注意力层输出后接上 (6)
上述 (8) 后再经过一个线性层得到对所有词汇的得分矩阵 \(\large X \in \mathbb{R}^{T' \times B \times V'}\)
注意力层结构
注意力层接收decoder的隐藏状态,目标序列词向量,encoder的输出。
保留一个残差 \(\large R \leftarrow X\) ,结合decoder的隐藏状态和目标序列词向量,\(\large X \leftarrow W^TX + emb_t ,\; X \in \mathbb{R}^{B \times T' \times E}\)
再与encoder的输出计算注意力得分矩阵 \(\large A \leftarrow X * O,\; A \in \mathbb{R}^{B \times T' \times T}\)
我们不需要 \(\large \langle pad \rangle\) 的产生注意,所以把 \(\large \langle pad \rangle\) 位置的得分都设置为负无穷
通过softmax对 \(\large A\) 计算注意力分布,得到对齐矩阵 \(\large A \leftarrow softmax(A)\)
论文中提到,对于注意力的输出,我们还需要计算一个conditional vector,\(\large Co \leftarrow A * U,\;Co \in \mathbb{R}^{B \times T' \times E}\)
最后加上残差后输出 \(\large X \leftarrow W^TX + R,\; X \in \mathbb{R}^{B \times C \times T'}\)
不同于RNN中所有时间步共享一个注意力层,这里的每一个卷积层后面都是一个独立的注意力层,当你有10层卷积层,那么就有10个独立的注意力层。
位置向量(Position Embeddings )
为了让卷积网络在处理序列时有一种空间感,我们要对词向量加上一个位置向量 \(\large emb \leftarrow emb + pos\_emb\)。其中 \(\large pos\_emb\) 表示对于词汇在该句子的索引编号。
初始化策略
- 为了抑制加上残差导致数值持续变大而导致高方差,所以每次加上残差或者加上词向量后,都乘以 \(\large \sqrt{0.5}\) 。
- 在获得词向量后和输入卷积块之前进行 \(\large p=0.1\) 的dropout正则化
- 对于卷积块的参数初始化,我们指定其正态分布 \(\large \mathcal{N}(0, \sqrt{4p/C})\),其中乘以 \(\large p\) 是为了抵消dropout时乘以的 \(\large 1/p\)。
- 线性层初始化参数符合 \(\large \mathcal{N}(0, \sqrt{(1-p)/N})\)
- 词向量和位置向量在 \(\large [0, 0.1]\) 之间均匀分布,并且 \(\large \langle pad \rangle\) 对应的词向量设为0
生成(Generation)
在训练时,我们可以一次性把整个目标句子输入到CNN中并行计算,不用像RNN中一步一步的输入,理论上的训练速度会有所提升,实际跑起来后会因为其中大量的注意力层会把训练速度拖慢。
在decoder生成预测序列时,我们需要以递进式的输入到CNN,需要输入 \(\large \frac{T(T-1)}{2}\) 次,而RNN逐个输入也就 \(\large T\) 次,所以生成速度上,CNN明显要慢。论文中提出的解决方案是把前面序列的卷积参数保留下来,不用重复计算,但并没有详细讲要怎么做,实现起来貌似难度挺大的。

Comments